AMC12竞赛考试内容
AMC12竞赛面向12年级及以下学生,与AMC10考试的题目与考察范围有很多重合的地方。参考国内数学课本,一般认为AMC12对应国内11年级的知识。
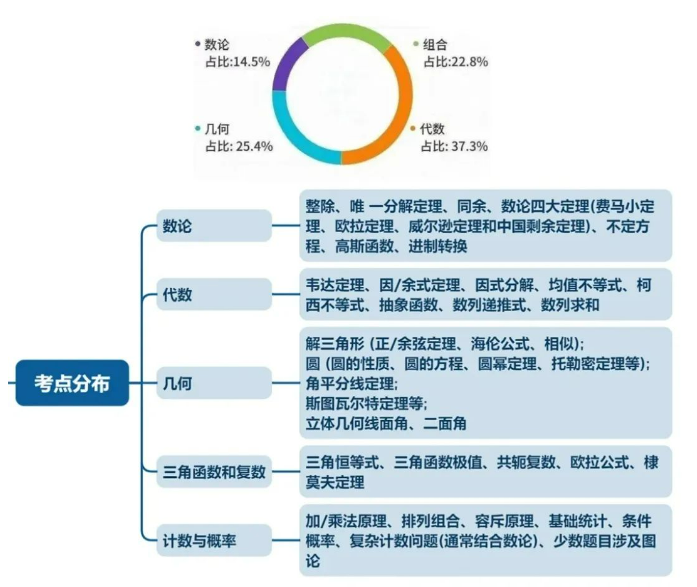
考察知识点以代数、组合、数论、几何四个模块为主,但核心知识层面上多出了对数、三角函数的计算与图像、复数三个知识模块的考察,并且这三个模块在AMC12中几乎100%会出题考察。
1.基本数论:
质数、分解质因数、整除法则(含余数法则)、最大公约数与最小公倍数、循环小数、分数等;
2.代数基础部分:
方程、不等式、韦达定理、指数和对数运算法则等;
3.数列:
等差数列、等比数列、复杂混合数列及逻辑推理等;
4.几何:
平行线、三角不等式、相似和全等三角形、三角形的高、中线和角平分线性质、正弦定理和余弦定理、四边形与多边形、圆、球体、长方体、正多面体;
5.函数:
一次函数、二次函数、绝对值函数、反函数、复合函数、三角和反三角函数、指数函数和对数函数、多项式函数等;
6.概率与统计:
集合、排列组合、二项展开定理、平均数、中位数、众数、方差和标准差等。
AMC12题目难度分布
AMC12包含25道选择题,题目大致按照由易到难的顺序排列,可以分为三个主要部分:
第1至15题
这些题目通常是较为基础和直接的问题,旨在测试学生对数学概念的理解和基本解题技巧。大多数认真准备并且熟悉相关数学知识点的学生应该能够正确解答这些问题。
第16至20题
这部分问题开始增加一些复杂度,并可能需要更深层次的思考和解题策略。这些题目往往能够区分出那些具备更强数学能力和更高水平的学生。这一阶段的题目对于中等偏上的学生来说具有挑战性,但仍然是可解决的。
第21至25题
最后几道题目通常是整个考试中最难的部分。它们不仅要求学生有扎实的数学基础知识,还需要创新性的思维和解决问题的能力。
2023年AMC12与历年难度对比表
| 对比 | 2022 10A | 2022 10B | 2021 10A Fall | 2021 10B Fall |
| 1-10 | 难度下降 | 难度上升 | 难度相当 | 难度相当 |
| 11-20 | 难度相当 | 难度下降 | 难度下降 | 难度下降 |
| 21-25 | 难度相当 | 难度相当 | 难度上升 | 难度相当 |
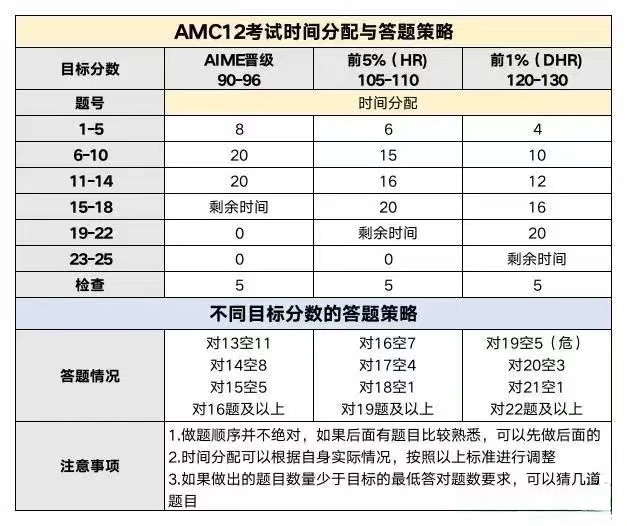
AMC12答题技巧
1. 设数法
适用场景:当方程个数少于变量个数时(不适用于整数方程),或者递推数列的前几项较大且复杂时。
操作方法:
假设某些变量为特定值,以简化问题。
对于递推数列,可以假设一些简单值或直接假设变量进行递推,观察是否存在周期性或明显规律。
2. 度量法
适用场景:部分几何题,尤其是当题目条件能够唯一确定图形时。
操作方法:
根据题目条件作出标准图或特殊情况下的图形。
通过度量边长、角度等直接得到答案。但需注意,近年来出题人可能会规避这种直接的度量方法,因此需谨慎使用。
3. 找规律
适用场景:递推数列、递推函数、新定义的数论函数、组合递推问题、二人游戏问题等。
操作方法:
从最简单的初始情况开始研究,逐步探索问题的本质。
仔细观察并尝试发现其中的规律,这有助于找到问题的解决方案。
4. 数形结合法
适用场景:函数与几何结合的问题。
操作方法:
将函数关系转化为图形表示,利用图形的直观性来解决问题。
同时,也可以将图形信息转化为函数表达式,以便进行更深入的分析。
5. 极端值法
适用场景:求最值问题或者范围问题。
操作方法:
考虑问题的极端情况,如最大值、最小值、边界值等。
通过分析极端情况下的问题表现,来推断出一般情况的解。
6. 排除法
适用场景:选择题或者有多个可能答案的问题。
操作方法:
根据已知条件和逻辑推理,排除明显错误的选项。
逐步缩小答案范围,直至找到正确答案。
AMC12与国内高考哪个难?

AMC12不需要用到微积分知识,而高考数学中部分题目可能需要用到极限和微积分的知识。此外,AMC112的计算量通常也不如高考数学大,但特别强调学生的读题理解能力,以及分析和解决问题的能力。
