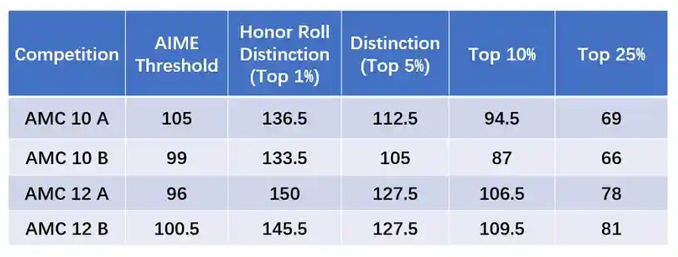
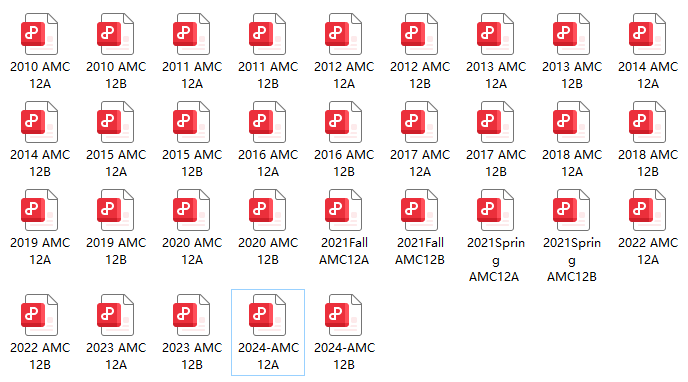
AMC12是为12年级及以下学生设计的数学竞赛,难度高于AMC10,涵盖更广泛的知识点。AMC12 数学竞赛不仅考察学生的数学知识广度,还考验其解题速度和思维深度。通过科学规划和系统准备,即使是普通学生也能在这一高水平竞赛中取得优异成绩。
一、AMC12四大模块的知识点详细分析及备考策略
1.代数模块(占比35%-40%)
基础衔接:AMC10核心代数考点回顾(多项式运算、函数与方程、数列与不等式基础)进阶拓展考点:
进阶拓展考点
不等式进阶:
柯西不等式、均值不等式(多元拓展)、绝对值不等式综合解法
多项式进阶:
有理根定理深化、韦达定理拓展(高次多项式)、多项式因式分解高阶技巧、多项式根的性质
函数进阶:
对数与指数函数综合应用、三角函数恒等变换(和差倍半公式、和积互化)、三角函数图像变换与性质深挖
复数:
运算规则、几何意义(复平面、模与辐角)、棣莫弗定理应用
模块命题规律
综合应用型题目占比高,常与几何、组合模块交叉综合应用。
2.几何模块(占比25%-30%)
基础衔接:AMC10核心几何考点回顾
平面几何定理:勾股定理、相似三角形等。
解析几何基础:直线、圆的标准方程及其性质。
立体几何基础:常见立体图形的表面积和体积计算。
进阶拓展考点
坐标几何进阶:
极坐标与参数方程(转化、应用)、直线与曲线的位置关系
立体几何进阶:
空间向量应用(夹角、距离计算)、外接球与内切球综合问题、空间几何体折叠与展开
圆的进阶性质:
圆内接多边形综合性质、幂函数进阶应用、圆与圆的位置关系深化
圆锥曲线基础:
椭圆、双曲线、抛物线的定义、标准方程与核心性质
模块命题规律
图形复杂度提升,需结合代数工具解题,空间想象能力要求高。
3.数论模块(占比15%-20%)
基础衔接:AMC10核心数论考点回顾
模运算:理解模运算的基本概念及其应用。
整除性:掌握整除性的判断方法。
质因数分解:熟练进行质因数分解。
同余方程基础:理解同余方程的基本概念及其解法。
进阶拓展考点
数论定理进阶:
欧拉定理、中国剩余定理进阶应用
不定方程:
高阶解法(无穷递降法、模分析)、特殊不定方程(佩尔方程基础)
数论函数:
欧拉函数、除数函数、高斯函数的性质与应用。
同余式进阶:
高次同余方程求解、同余式组综合应用
模块命题规律
题目隐蔽性强,需熟练掌握数论工具的灵活应用。
4.组合数学模块(占比15%-20%)
基础衔接:AMC10核心组合考点回顾
排列组合:掌握排列组合的基本概念及其应用。
概率统计基础:理解概率的基本概念及其计算方法。
递推关系:掌握递推关系的基本概念及其应用。
容斥原理基础:理解容斥原理的基本概念及其应用。
进阶拓展考点
计数进阶:
生成函数(普通生成函数、指数生成函数)、容斥原理高阶应用
递推关系进阶:
线性递推关系求解、非线性递推关系初步
概率进阶:
条件概率综合应用、期望与方差计算(离散型随机变量)、概率模型拓展
组合几何初步:
图形计数、区域划分问题
模块命题规律
逻辑推理要求高,常结合实际场景命题,方法多样性强。
二、AMC10/12长线备考全攻略
第一阶段(现在-6月):搭建知识体系,夯实基础
明确考察占比范围:
代数:占30%(函数、方程、数列等)
几何:占25%(三角形、圆、立体几何等)
数论和组合:各占20%-25%
根据自身强弱项分配时间:制定个性化学习计划,重点突破薄弱环节。
第二阶段(7月-9月):真题精刷,训练答题节奏
精选近几年AMC10/12真题,按“三遍刷题法”训练:
第一遍限时模考:严格按照75分钟完成,模拟真实考试状态。
第二遍分类重做错题:总结不同题型的解题套路。
第三遍专攻21-25题的压轴题:突破思维瓶颈。
训练答题策略:
前10题基础题保证100%正确率。
11-20题中档题控制失误。
21-25题合理分配时间,避免因纠结难题而错失基础分。
第三阶段(10月-考前):错题复盘,冲刺拔高
建立专属错题本:
记录每道错题的错误类型(计算失误/概念混淆/策略错误)、考点归属(如“数论-中国剩余定理”)、正确思路和类似题型链接。
每周复盘一次,做到举一反三。
进行整套真题模拟:
调整答题节奏和心态,针对高频考点和易错点进行专项突破。
如果想冲击前1%,可以额外针对性训练AIME真题,提升综合解题能力。
扫码进入 AMC 12 专属学习社群,海量备赛资料&体验课程等你开启!
扫码免费领AMC 12 备赛资料包⇓
(内含AMC 12 历年真题+解析+书单+公式等)

AMC12辅导课程
授课教师均来自全球名校,结合精准课程规划与全程学习跟踪,全程护航提分夺奖!
| 班型 | 课时 | 人数 | 开课时间 |
| 寒假班 | 30H | 3-8人 | 详询老师 |
| 系统课 | 20H | 1v1/3-8人班 | 详询老师 |
| 刷题班 | 20H | 1v1/3-8人班 | 详询老师 |

扫码了解AMC10/12竞赛课程
可免费领取自研精编讲义