2025年AMC12竞赛分数线的“暴涨”现象让许多家长和学生感到困惑。本文将深入剖析分数线暴涨的原因,并提供不同基础学生的备考规划,帮助你在2026年的竞赛中取得理想成绩。
一、AMC12分数线暴涨的两大原因揭秘
原因一:考题失误全员赋分
事件背景:
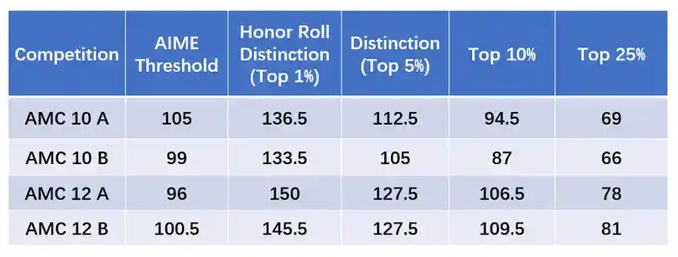
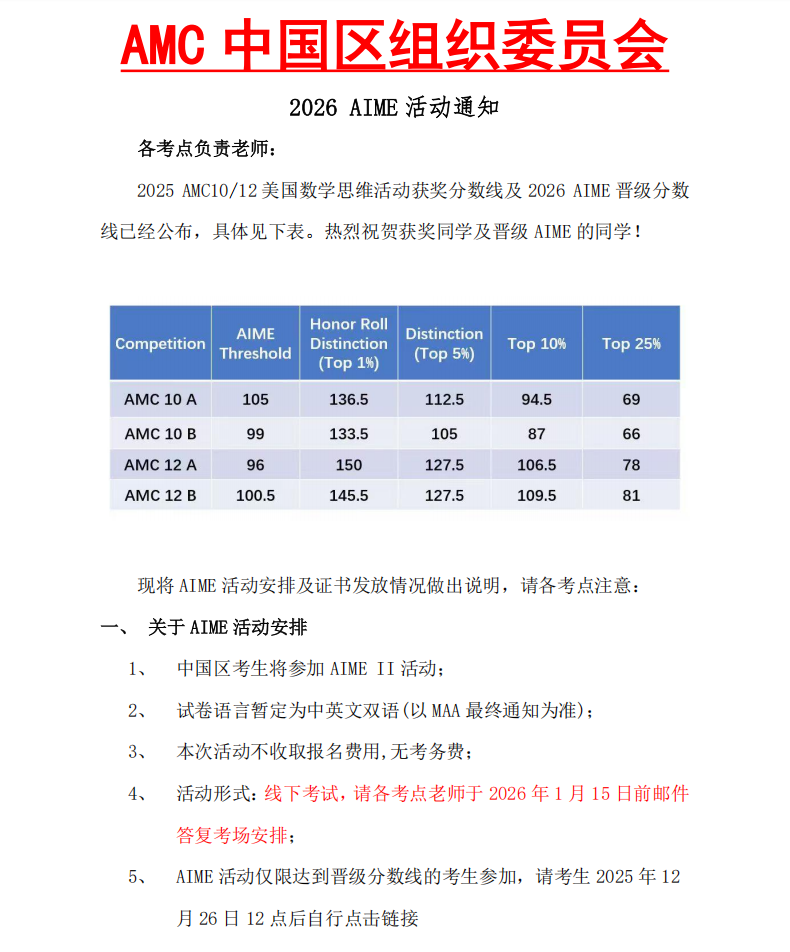
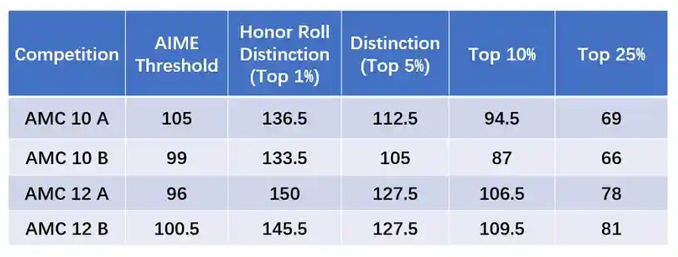
在2025年AMC12美区A卷考试中,某道题目出现了出题失误,给出的五个选项中均没有正确答案。
处理结果:
MAA组委会核实问题后,决定对所有考生在这道题上给予6分满分。由于AMC12的分数线是根据美国学生的成绩进行划分的,这次全员赋分导致了前1%分数线飙升至满分150分!
这种情况虽然罕见,但也提醒我们:官方评分标准可能会因特殊情况而调整,因此在备考时要注重全面准备,而不是押宝个别题目。
原因二:泄题现象依旧存在
现状分析:
泄题问题虽然未完全杜绝,但官方在中国考区已采取多项措施加以防范:
推行线下考试;
采用多套试卷;
计划于2026年2月出台新规严打作弊现象。
公信力修复:
随着这些措施的逐步实施,AMC竞赛的公信力正在逐步恢复,其作为国际认可度极高的数学竞赛的地位依然稳固。
二、AMC12依旧值得参加的三大理由
硬核背书
对于申请MIT、斯坦福、牛津、剑桥等顶尖名校的学生来说,AMC12高分+晋级AIME是强有力的学术背书,能显著提升竞争力。
成绩需真实匹配
AMC12高分需要与其他学术表现(如AIME成绩、AL/IB数学成绩)相匹配。若出现明显脱节(如AMC12满分但AIME成绩不理想),可能引发招生官对申请材料真实性的质疑。
学科反哺显著
备考过程中积累的数学思维和知识,不仅能帮助你应对竞赛,还能实实在在地提升校内学习中的学科能力。
三、2026年AMC12基本赛制概览
考试时间
预计为2026年11月(具体日期待官方公布)
参赛资格
12年级(高三)及以下且≤19.5周岁的学生
考试形式
25道单选题,每题6分,答错不得分,不答得1.5分,满分150分
考试时长:75分钟
A/B卷说明:
A/B卷是不同的试卷,但难度和考试范围相近;
考生可以选择A卷或B卷考试,也可以两场都参加,最终取最高成绩参与评奖排名和晋级AIME。
考点汇总
代数:9-10道题,涵盖复杂不等式、柯西不等式、复杂函数问题等;
几何:6-8道题,涉及立体几何、平面几何等;
数论:4-6道题,包括欧拉公式、费马小定理等;
组合与概率:3-5道题,涵盖排列组合、递推关系等。
四、不同基础学生的AMC12备考规划
1.零基础备考AMC12竞赛
备考重点
梳理AMC12竞赛基础知识,形成完整的知识框架;
掌握四大模块(代数、几何、数论、组合)的基础知识点。
建议备考周期
8-12个月
推荐课程
AMC12直通车课程
2.参加过AMC10竞赛备考AMC12竞赛
备考重点
拓展AMC12竞赛的知识点,尤其是新增的复杂不等式、柯西不等式、复杂函数问题、欧拉公式、费马小定理等内容;
强化数论与组合部分的学习。
建议备考周期
6-8个月
推荐课程
AMC12优享班
3.非首次参加AMC12竞赛
备考重点
针对性巩固,总结以往AMC12竞赛中的常错考点以及不熟悉的考点;
进行拓展强化训练,提升解题速度与准确性。
建议备考周期
4-6个月
推荐课程
AMC12强化冲刺班
扫码进入 AMC 12 专属学习社群,海量备赛资料&体验课程等你开启!
扫码免费领AMC 12 备赛资料包⇓
(内含AMC 12 历年真题+解析+书单+公式等)

AMC12辅导课程
授课教师均来自全球名校,结合精准课程规划与全程学习跟踪,全程护航提分夺奖!
| 班型 | 课时 | 人数 | 开课时间 |
| 寒假班 | 30H | 3-8人 | 详询老师 |
| 系统课 | 20H | 1v1/3-8人班 | 详询老师 |
| 刷题班 | 20H | 1v1/3-8人班 | 详询老师 |

扫码了解AMC10/12竞赛课程
可免费领取自研精编讲义